Găsiți centrul de greutate al unui corp plat de formă neregulată. Pozițiile centrului de greutate al unor figuri

6.1. Informații generale

Centrul Forțelor Paralele
Să considerăm două forțe paralele direcționate într-o direcție și , aplicate corpului în puncte A 1 și A 2 (Fig.6.1). Acest sistem de forțe are o rezultantă, a cărei linie de acțiune trece printr-un anumit punct CU. Poziția punctului CU poate fi găsit folosind teorema lui Varignon:

Dacă întoarceți forțele și aproape de puncte A 1 și A 2 într-o direcție și în același unghi, apoi obținem un nou sistem de salas paralele având aceleași module. În acest caz, rezultanta lor va trece și prin punct CU. Acest punct se numește centrul forțelor paralele.
Să considerăm un sistem de forțe paralele și direcționate identic aplicate unui corp solid în puncte. Acest sistem are o rezultată.
Dacă fiecare forță a sistemului este rotită în apropierea punctelor de aplicare a acestora în aceeași direcție și la același unghi, atunci se vor obține noi sisteme de forțe paralele identic direcționate cu aceleași module și puncte de aplicare. Rezultanta unor astfel de sisteme va avea același modul R, dar de fiecare dată o direcție diferită. După ce mi-am împăturit puterile F 1 și F 2 constatăm că rezultanta lor R 1, care va trece întotdeauna prin punct CU 1, a cărui poziţie este determinată de egalitatea . Pliere mai departe R 1 și F 3, găsim rezultanta lor, care va trece întotdeauna prin punct CU 2 culcat pe o linie dreaptă A 3 CU 2. După ce am terminat procesul de adăugare a forțelor până la final, vom ajunge la concluzia că rezultanta tuturor forțelor va trece într-adevăr întotdeauna prin același punct. CU, a cărui poziţie în raport cu punctele va fi neschimbată.
Punct CU, prin care trece linia de acțiune a sistemului rezultant de forțe paralele pentru orice rotație a acestor forțe în apropierea punctelor de aplicare a acestora în aceeași direcție la același unghi se numește centru de forțe paralele (fig. 6.2).

Fig.6.2

Să determinăm coordonatele centrului de forțe paralele. De la poziţia punctului CU relativ la corp este neschimbată, atunci coordonatele sale nu depind de alegerea sistemului de coordonate. Să întoarcem toate forțele în jurul aplicării lor, astfel încât acestea să devină paralele cu axa OUși aplicați teorema lui Varignon forțelor rotite. Deoarece R" este rezultanta acestor forțe, atunci, conform teoremei lui Varignon, avem , deoarece , , primim

De aici găsim coordonatele centrului forțelor paralele zc:

Pentru a determina coordonatele xc Să creăm o expresie pentru momentul forțelor în jurul axei Oz.

Pentru a determina coordonatele Y c să întoarcem toate forțele astfel încât să devină paralele cu axa Oz.

Poziția centrului forțelor paralele față de origine (Fig. 6.2) poate fi determinată de vectorul său rază:

6.2. Centrul de greutate al unui corp rigid

Centrul de greutate a unui corp rigid este un punct asociat invariabil cu acest corp CU, prin care trece linia de acțiune a forțelor de gravitație rezultante ale unui corp dat, pentru orice poziție a corpului în spațiu.
Centrul de greutate este utilizat în studierea stabilității pozițiilor de echilibru ale corpurilor și mediilor continue sub influența gravitației și în alte cazuri, și anume: în rezistența materialelor și în mecanica structurală - atunci când se utilizează regula lui Vereshchagin.
Există două moduri de a determina centrul de greutate al unui corp: analitic și experimental. Metoda analitică pentru determinarea centrului de greutate decurge direct din conceptul de centru de forțe paralele.
Coordonatele centrului de greutate, ca centru al forțelor paralele, sunt determinate de formulele:

Unde R- greutatea întregului corp; pk- greutatea particulelor corporale; xk, yk, zk- coordonatele particulelor corporale.
Pentru un corp omogen, greutatea întregului corp și a oricărei părți a acestuia este proporțională cu volumul P=Vy, pk =vk γ, Unde γ - greutate pe unitate de volum, V- volumul corpului. Înlocuirea expresiilor P, pkîn formula de determinare a coordonatelor centrului de greutate și, reducând printr-un factor comun γ , primim:

Punct CU, ale cărui coordonate sunt determinate de formulele rezultate, se numește centrul de greutate al volumului.
Dacă corpul este o placă subțire omogenă, atunci centrul de greutate este determinat de formulele:

Unde S- suprafața întregii plăci; sk- suprafața părții sale; xk, da- coordonatele centrului de greutate al pieselor de placă.
Punct CU in acest caz se numeste zona centrului de greutate.
Număratorii expresiilor care determină coordonatele centrului de greutate al figurilor plane se numesc cu momente statice ale zonei raportat la axe laȘi X:

Apoi, centrul de greutate al zonei poate fi determinat prin formulele:

Pentru corpurile a căror lungime este de multe ori mai mare decât dimensiunile secțiunii transversale, determinați centrul de greutate al liniei. Coordonatele centrului de greutate al liniei sunt determinate de formulele:

Unde L- lungimea liniei; lk- lungimea părților sale; xk, yk, zk- coordonata centrului de greutate al unor părți ale liniei.

6.3. Metode de determinare a coordonatelor centrelor de greutate ale corpurilor

Pe baza formulelor obținute se pot propune metode practice de determinare a centrelor de greutate a corpurilor.
1. Simetrie. Dacă un corp are un centru de simetrie, atunci centrul de greutate se află în centrul de simetrie.
Dacă corpul are un plan de simetrie. De exemplu, planul XOU, apoi centrul de greutate se află în acest plan.
2. Despicare. Pentru corpurile formate din corpuri de formă simplă se folosește metoda despărțirii. Corpul este împărțit în părți, al căror centru de greutate este determinat de metoda simetriei. Centrul de greutate al întregului corp este determinat de formulele pentru centrul de greutate al volumului (ariei).

Exemplu. Determinați centrul de greutate al plăcii prezentate în figura de mai jos (Fig. 6.3). Placa poate fi împărțită în dreptunghiuri în diferite moduri și se pot determina coordonatele centrului de greutate al fiecărui dreptunghi și aria acestora.

Fig.6.3

Răspuns: Xc=17,0 cm; yc= 18,0 cm.

3. Plus. Această metodă este un caz special al metodei de partiționare. Se folosește atunci când corpul are decupaje, felii etc., dacă se cunosc coordonatele centrului de greutate al corpului fără decupaj.

Exemplu. Determinați centrul de greutate al unei plăci circulare având o rază de decupare r = 0,6 R(Fig. 6.4).

Fig.6.4

O placă rotundă are un centru de simetrie. Să plasăm originea coordonatelor în centrul plăcii. Zona farfurii fără decupaj, zonă decupată. Farfurie patrata cu decupaj; .
Placa cu decupaj are o axă de simetrie О1 x, prin urmare, Y c=0.

4. Integrare. Dacă corpul nu poate fi împărțit într-un număr finit de părți, ale căror poziții ale centrelor de greutate sunt cunoscute, corpul este împărțit în volume mici arbitrare, pentru care formula folosind metoda de împărțire ia forma: .
Apoi merg la limită, direcționând volumele elementare la zero, adică. contractarea volumelor în puncte. Sumele sunt înlocuite cu integrale extinse pe întregul volum al corpului, apoi formulele de determinare a coordonatelor centrului de greutate al volumului iau forma:

Formule pentru determinarea coordonatelor centrului de greutate al unei zone:

Coordonatele centrului de greutate al zonei trebuie determinate atunci când se studiază echilibrul plăcilor, când se calculează integrala Mohr în mecanica structurală.

Exemplu. Determinați centrul de greutate al unui arc de cerc de rază R cu unghi central AOB= 2α (Fig. 6.5).

Orez. 6.5

Arcul de cerc este simetric cu axa Oh, prin urmare, centrul de greutate al arcului se află pe axă Oh, yс = 0.
Conform formulei pentru centrul de greutate al unei linii:

6.Metoda experimentala. Centrele de greutate ale corpurilor neomogene de configurație complexă pot fi determinate experimental: prin metoda suspendării și cântăririi. Prima metodă este suspendarea corpului pe un cablu în diferite puncte. Direcția cablului de care este suspendat corpul va da direcția gravitației. Punctul de intersecție al acestor direcții determină centrul de greutate al corpului.
Metoda de cântărire presupune mai întâi determinarea greutății unei caroserii, cum ar fi o mașină. Apoi presiunea axei din spate a vehiculului pe suport este determinată pe cântar. Întocmind o ecuație de echilibru în raport cu un punct, de exemplu, axa roților din față, puteți calcula distanța de la această axă la centrul de greutate al mașinii (Fig. 6.6).

Fig.6.6

Uneori, atunci când rezolvați probleme, este necesar să folosiți simultan diferite metode pentru determinarea coordonatelor centrului de greutate.

6.4. Centrele de greutate ale unor figuri geometrice simple

Pentru a determina centrele de greutate ale corpurilor de forme care apar frecvent (triunghi, arc de cerc, sector, segment), este convenabil să folosiți date de referință (Tabelul 6.1).

Tabelul 6.1

Coordonatele centrului de greutate al unor corpuri omogene

Notă. Centrul de greutate al unei figuri simetrice se află pe axa de simetrie.

Centrul de greutate al tijei este la mijlocul înălțimii. Pentru rezolvarea problemelor se folosesc următoarele metode:

1. metoda simetriei: centrul de greutate al figurilor simetrice este pe axa de simetrie;

2. metoda de separare: secțiunile complexe sunt împărțite în mai multe părți simple, a căror poziție a centrelor de greutate este ușor de determinat;

3. metoda zonei negative: cavitățile (găurile) sunt considerate ca parte a unei secțiuni cu zonă negativă.

Exemple de rezolvare a problemelor

Exemplul 1. Determinați poziția centrului de greutate al figurii prezentate în fig. 8.4.

Soluţie

Împărțim figura în trei părți:

Definit în mod similar la C = 4,5 cm.

Exemplul 2. Găsiți poziția centrului de greutate al unei ferme de bare simetrice ADBE(Fig. 116), ale căror dimensiuni sunt următoarele: AB = 6m, DE = 3 m și EF = 1m.

Soluţie

Întrucât împrejmuirea este simetrică, centrul său de greutate se află pe axa de simetrie D.F. Cu sistemul de axe de coordonate selectat (Fig. 116), abscisa centrului de greutate al fermei

În consecință, doar ordonata este necunoscută la C centrul de greutate al fermei. Pentru a o determina, împărțim ferme în părți separate (tije). Lungimile lor sunt determinate din triunghiurile corespunzătoare.

Din ΔAEF avem

Din ΔADF avem

Centrul de greutate al fiecărei tije se află în mijlocul ei, coordonatele acestor centre sunt ușor de determinat din desen (Fig. 116).

Lungimile și ordonatele găsite ale centrelor de greutate ale părților individuale ale fermei sunt introduse în tabel și conform formulei

determina ordonata y s centrul de greutate al unei ferme plane date.

Prin urmare, centrul de greutate CUîntreaga ferme se află pe axă DF simetria fermei la o distanţă de 1,59 m de punct F.

Exemplul 3. Determinați coordonatele centrului de greutate al secțiunii compozite. Secțiunea este formată dintr-o foaie și profile laminate (Fig. 8.5).

Notă. Adesea, cadrele sunt sudate din diferite profile pentru a crea structura necesară. Astfel, se reduce consumul de metal și se formează o structură de înaltă rezistență.

Pentru profilele laminate standard, se cunosc propriile caracteristici geometrice. Ele sunt date în standardele relevante.

Soluţie

1. Să desemnăm cifrele prin numere și să scriem datele necesare din tabele:

1 - canalul nr. 10 (GOST 8240-89); înălţime h = 100 mm; latimea raftului b= 46 mm; arie a secțiunii transversale A 1= 10,9 cm2;

2 - grindă în I nr. 16 (GOST 8239-89); inaltime 160 mm; latime raft 81 mm; aria secțiunii transversale A 2 - 20,2 cm 2;

3 - foaie 5x100; grosime 5 mm; latime 100 mm; aria secțiunii transversale A 3 = 0,5 10 = 5 cm 2.

2. Coordonatele centrelor de greutate ale fiecărei figuri pot fi determinate din desen.

Secțiunea compozită este simetrică, deci centrul de greutate este pe axa de simetrie și coordonatele X C = 0.

3. Determinarea centrului de greutate al unei secțiuni compozite:

Exemplul 4. Determinați coordonatele centrului de greutate al secțiunii prezentate în fig. 8, A. Secțiunea este formată din două unghiuri 56x4 și canalul nr. 18. Verificați corectitudinea determinării poziției centrului de greutate. Indicați poziția sa pe secțiune.

Soluţie

1. : două colțuri 56 x 4 și canalul nr. 18. Să le notăm 1, 2, 3 (vezi Fig. 8, A).

2. Indicăm centrele de greutate fiecare profil, folosind tabelul 1 și 4 adj. eu, și le denotă C 1, C 2, C 3.

3. Selectați un sistem de axe de coordonate. Axă la compatibil cu axa de simetrie și cu axa X trageți prin centrele de greutate ale colțurilor.

4. Determinați coordonatele centrului de greutate al întregii secțiuni. Din moment ce axa la coincide cu axa de simetrie, apoi trece prin centrul de greutate al secțiunii, prin urmare x s= 0. Coordonată y s vom determina prin formula

Folosind tabelele din anexă, determinăm ariile fiecărui profil și coordonatele centrelor de greutate:

Coordonatele la 1Și la 2 sunt egale cu zero, deoarece axa X trece prin centrele de greutate ale colțurilor. Să înlocuim valorile obținute în formula pentru a determina y s:

5. Să indicăm centrul de greutate al secțiunii din fig. 8, a și notați-l cu litera C. Să arătăm distanța y C = 2,43 cm de la axă X la punctul C.

Deoarece colțurile sunt situate simetric și au aceeași zonă și coordonate, atunci A 1 = A 2, y 1 = y 2. Prin urmare, formula de determinare la C poate fi simplificat:

6. Sa verificam.În acest scop axa X Să desenăm de-a lungul marginii inferioare a raftului de colț (Fig. 8, b). Axă la Să lăsăm ca în prima soluție. Formule de determinare x CȘi la C nu schimba:

Zonele profilelor vor rămâne aceleași, dar coordonatele centrelor de greutate ale unghiurilor și canalelor se vor schimba. Să le scriem:

Aflați coordonatele centrului de greutate:

După coordonatele găsite x sȘi y s trageți pe desen punctul C. Poziția centrului de greutate găsită în două moduri este în același punct. Hai să verificăm. Diferența între coordonate da s, găsită în prima și a doua soluție este: 6,51 - 2,43 = 4,08 cm.

Aceasta este egală cu distanța dintre axa x din prima și a doua soluție: 5,6 - 1,52 = 4,08 cm.

Răspuns: s= 2,43 cm dacă axa x trece prin centrele de greutate ale colțurilor sau y c = 6,51 cm dacă axa x trece de-a lungul marginii inferioare a flanșei de colț.

Exemplul 5. Determinați coordonatele centrului de greutate al secțiunii prezentate în fig. 9, A. Secțiunea constă din fasciculul I nr. 24 și canalul nr. 24a. Arată poziția centrului de greutate pe secțiune.

Soluţie

1.Să împărțim secțiunea în profile laminate: I-beam și canal. Să le notăm cu numerele 1 și 2.

3. Indicăm centrele de greutate ale fiecărui profil C 1 și C 2 folosind tabele de aplicare.

4. Selectați un sistem de axe de coordonate. Axa x este compatibilă cu axa de simetrie, iar axa y este trasă prin centrul de greutate al fasciculului I.

5. Determinați coordonatele centrului de greutate al secțiunii. Coordonata y c = 0, deoarece axa X coincide cu axa de simetrie. Determinăm coordonata x cu formula

Conform tabelului 3 și 4 adj. I și diagrama în secțiune transversală pe care o determinăm

Să înlocuim valorile numerice în formulă și să obținem

5. Să trasăm punctul C (centrul de greutate al secțiunii) folosind valorile găsite ale lui x c și y c (vezi Fig. 9, a).

Soluția trebuie verificată independent cu axele poziționate așa cum se arată în Fig. 9, b. Ca rezultat al soluției, obținem x c = 11,86 cm Diferența dintre valorile lui x c pentru prima și a doua soluție este de 11,86 - 6,11 = 5,75 cm, care este egală cu distanța dintre axele y pentru aceeași solutii b dv /2 = 5,75 cm.

Răspuns: x c = 6,11 cm, dacă axa y trece prin centrul de greutate al fasciculului I; x c = 11,86 cm dacă axa y trece prin punctele extreme din stânga ale fasciculului I.

Exemplul 6. Macaraua feroviară se sprijină pe șine, distanța dintre care este AB = 1,5 m (Fig. 1.102). Forța gravitațională a căruciorului cu macara este G r = 30 kN, centrul de greutate al căruciorului este în punctul C, situat pe dreapta KL de intersecție a planului de simetrie al căruciorului cu planul desenului. Forța gravitațională a troliului macaralei Q l = 10 kN se aplică în punct D. Forța gravitațională a contragreutății G„=20 kN se aplică în punctul E. Forța gravitațională a brațului G c = 5 kN se aplică în punctul H. Extinderea macaralei față de linia KL este de 2 m. Determinați coeficientul de stabilitate al macaralei în stare fără sarcină și ce sarcină F poate fi ridicat cu aceasta macara, cu conditia ca coeficientul de stabilitate sa fie de cel putin doi.

Soluţie

1. Când este descărcată, macaraua riscă să se răstoarne când se întoarce în jurul șinei A. Prin urmare, relativ la punct A moment de stabilitate

2. Moment de răsturnare relativ la un punct A este creat de forța gravitațională a contragreutății, adică

3. De aici coeficientul de stabilitate al macaralei in stare neincarcata

4. La încărcarea brațului macaralei cu încărcătură F există pericolul de răsturnare a macaralei la întoarcerea lângă șina B. Prin urmare, raportat la punct ÎN moment de stabilitate

5. Moment de răsturnare față de șină ÎN

6. În funcție de condițiile problemei, este permisă funcționarea macaralei cu un coeficient de stabilitate k B ≥ 2, adică.

Testați întrebări și sarcini

1. De ce forțele de atracție către Pământ care acționează asupra punctelor corpului pot fi luate ca un sistem de forțe paralele?

2. Notează formule pentru determinarea poziţiei centrului de greutate al corpurilor neomogene şi omogene, formule pentru determinarea poziţiei centrului de greutate al secţiunilor plane.

3. Repetați formulele pentru determinarea poziției centrului de greutate al formelor geometrice simple: dreptunghi, triunghi, trapez și semicerc.

4.
Care este momentul static al ariei?

5. Calculați momentul static al acestei figuri în jurul axei Bou. h= 30 cm; b= 120 cm; Cu= 10 cm (Fig. 8.6).

6. Determinați coordonatele centrului de greutate al figurii umbrite (Fig. 8.7). Dimensiunile sunt date in mm.

7. Determinați coordonatele la figura 1 a secțiunii compozite (Fig. 8.8).

Când decideți, utilizați datele de referință din tabelele GOST „Oțel laminat la cald” (vezi Anexa 1).

Determinarea centrului de greutate al unui corp arbitrar prin adăugarea secvențială a forțelor care acționează asupra părților sale individuale este o sarcină dificilă; devine mai ușor doar pentru corpurile de formă relativ simplă.

Fie ca corpul să fie format din doar două mase și conectat printr-o tijă (Fig. 125). Dacă masa tijei este mică în comparație cu masele și , atunci poate fi neglijată. Fiecare dintre mase este acţionată de forţe gravitaţionale egale cu şi respectiv; ambele sunt îndreptate vertical în jos, adică paralele între ele. După cum știm, rezultanta a două forțe paralele este aplicată la un punct, care este determinată din condiție

Orez. 125. Determinarea centrului de greutate al unui corp format din două sarcini

În consecință, centrul de greutate împarte distanța dintre două sarcini într-un raport invers raportului dintre masele lor. Dacă acest corp este suspendat în punctul , va rămâne în echilibru.

Deoarece două mase egale au un centru de greutate comun într-un punct care bisectează distanța dintre aceste mase, este imediat clar că, de exemplu, centrul de greutate al unei tije omogene se află în mijlocul tijei (Fig. 126).

Deoarece orice diametru al unui disc rotund omogen îl împarte în două părți simetrice complet identice (Fig. 127), centrul de greutate trebuie să se afle pe fiecare diametru al discului, adică în punctul de intersecție al diametrelor - în centrul geometric al discul. Raționând într-un mod similar, putem constata că centrul de greutate al unei bile omogene se află în centrul său geometric, centrul de greutate al unui paralelipiped dreptunghiular uniform se află la intersecția diagonalelor sale etc. Centrul de greutate al unui cerc. sau inelul se află în centrul său. Ultimul exemplu arată că centrul de greutate al unui corp se poate afla în afara corpului.

Orez. 126. Centrul de greutate al unei tije omogene se află în mijlocul ei

Orez. 127. Centrul unui disc omogen se află în centrul său geometric

Dacă corpul are o formă neregulată sau dacă este eterogen (de exemplu, are goluri), atunci calcularea poziției centrului de greutate este adesea dificilă și este mai convenabil să găsiți această poziție prin experiment. De exemplu, doriți să găsiți centrul de greutate al unei bucăți de placaj. Să-l atârnăm pe un fir (Fig. 128). Evident, în poziția de echilibru, centrul de greutate al corpului trebuie să se afle pe prelungirea firului, altfel forța gravitației va avea un moment relativ la punctul de suspensie, care ar începe să rotească corpul. Prin urmare, trasând pe bucata noastră de placaj o linie dreaptă, reprezentând continuarea firului, putem spune că centrul de greutate se află pe această linie dreaptă.

Într-adevăr, suspendând corpul în puncte diferite și trasând linii verticale, ne vom asigura că toate se intersectează într-un punct. Acest punct este centrul de greutate al corpului (deoarece trebuie să se afle simultan pe toate astfel de linii). Într-un mod similar, puteți determina poziția centrului de greutate nu numai a unei figuri plate, ci și a unui corp mai complex. Poziția centrului de greutate al aeronavei este determinată prin rularea roților pe platforma de cântărire. Rezultanta forțelor de greutate exercitate asupra fiecărei roți va fi direcționată vertical, iar linia de-a lungul căreia acţionează poate fi găsită folosind legea adunării forţelor paralele.

Orez. 128. Punctul de intersecție al liniilor verticale trasate prin punctele de suspensie este centrul de greutate al corpului

Când masa părților individuale ale corpului se modifică sau când se schimbă forma corpului, poziția centrului de greutate se schimbă. Astfel, centrul de greutate al aeronavei se mișcă atunci când se consumă combustibil din rezervoare, la încărcarea bagajelor etc. Pentru un experiment vizual care ilustrează mișcarea centrului de greutate când se schimbă forma corpului, este convenabil să luați două bare identice legate printr-o balama (Fig. 129). În cazul în care barele formează o continuare între ele, centrul de greutate se află pe axa barelor. Dacă barele sunt îndoite la balama, atunci centrul de greutate este în afara barelor, pe bisectoarea unghiului pe care îl formează. Dacă puneți o sarcină suplimentară pe una dintre bare, centrul de greutate se va deplasa spre această sarcină.

Orez. 129. a) Centrul de greutate al barelor conectate printr-o balama, situat pe o linie dreaptă, se află pe axa barelor, b) Centrul de greutate al unui sistem îndoit de bare se află în afara barelor

81.1. Unde este centrul de greutate a două tije subțiri identice având o lungime de 12 cm și prinse în forma literei T?

81.2. Demonstrați că centrul de greutate al unei plăci triunghiulare omogene se află la intersecția medianelor.

Orez. 130. Pentru exercițiul 81.3

81.3. O placă omogenă cu masa de 60 kg se sprijină pe două suporturi, așa cum se arată în Fig. 130. Determinaţi forţele care acţionează asupra suporturilor.

Centrul de greutate al unui corp solid este un punct geometric care este legat rigid de acest corp și este centrul forțelor gravitaționale paralele aplicate particulelor elementare individuale ale corpului (Figura 1.6).

Vector raza acestui punct

Figura 1.6

Pentru un corp omogen, poziția centrului de greutate al corpului nu depinde de material, ci este determinată de forma geometrică a corpului.

Dacă greutatea specifică a unui corp omogen γ , greutatea unei particule elementare a corpului

P k = yΔV k (P = γV ) înlocuiți în formula pentru a determina r C , avem

De unde, proiectand pe axe si trecand la limita, obtinem coordonatele centrului de greutate al unui volum omogen.

În mod similar pentru coordonatele centrului de greutate al unei suprafețe omogene cu arie S (Figura 1.7, a)

Figura 1.7

Pentru coordonatele centrului de greutate al unei linii omogene de lungime L (Figura 1.7, b)

Metode de determinare a coordonatelor centrului de greutate

Pe baza formulelor generale obținute mai devreme, putem indica metode pentru determinarea coordonatelor centrelor de greutate ale corpurilor solide:

1 Analitic(prin integrare).

2 Metoda simetriei. Dacă un corp are un plan, o axă sau un centru de simetrie, atunci centrul său de greutate se află, respectiv, în planul de simetrie, axa de simetrie sau centrul de simetrie.

3 Experimental(metoda de agățare a corpului).

4 Despicare. Corpul este împărțit într-un număr finit de părți, pentru fiecare dintre ele poziția centrului de greutate C si zona S cunoscut. De exemplu, proiecția unui corp pe un plan xOy (Figura 1.8) poate fi reprezentat ca două figuri plate cu zone S 1 Și S 2 (S=S 1 +S 2 ). Centrele de greutate ale acestor figuri sunt situate în puncte C 1 (X 1 , y 1 ) Și C 2 (X 2 , y 2 ) . Atunci coordonatele centrului de greutate al corpului sunt egale

Figura 1.8

5Plus(metoda suprafețelor sau volumelor negative). Un caz special al metodei de partiționare. Se aplică corpurilor care au decupaje dacă sunt cunoscute centrele de greutate ale corpului fără decupaj și partea decupată. De exemplu, trebuie să găsiți coordonatele centrului de greutate al unei figuri plate (Figura 1.9):

Figura 1.9

Centrele de greutate ale celor mai simple figuri

Figura 1.10

1 Triunghi

Centrul de greutate al ariei triunghiului coincide cu punctul de intersecție al medianelor sale (Figura 1.10, a).

DM = MB , CM= (1/3)A.M. .

2 Arc de cerc

Arcul are o axă de simetrie (Figura 1.10, b). Centrul de greutate se află pe această axă, adică y C = 0 .

dl – element arc, dl = Rdφ , R – raza cercului, x = Rcosφ , L= 2αR ,

Prin urmare:

X C = R(sinα/α) .

3 Sector circular

Sectorul de rază R cu unghi central 2 α are o axă de simetrie Bou , pe care se află centrul de greutate (Figura 1.10, c).

Împărțim sectorul în sectoare elementare, care pot fi considerate triunghiuri. Centrele de greutate ale sectoarelor elementare sunt situate pe un arc de cerc de rază (2/3) R .

Centrul de greutate al sectorului coincide cu centrul de greutate al arcului AB :

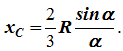
14. Metode de precizare a mișcării unui punct.

Cu metoda vectorială de specificare a mișcării, poziția unui punct este determinată de un vector cu rază desenat dintr-un punct fix în sistemul de referință selectat.

Cu metoda coordonatelor de specificare a mișcării, coordonatele unui punct sunt specificate în funcție de timp:

Acestea sunt ecuații parametrice ale traiectoriei unui punct în mișcare, în care timpul joacă rolul unui parametru t . Pentru a-și scrie ecuația în formă explicită, este necesar să excludem din ele t .

Cu metoda naturală de specificare a mișcării, se specifică traiectoria punctului, originea referinței pe traiectorie care indică direcția pozitivă a referinței și legea modificării coordonatei arcului: s=s(t) . Această metodă este convenabilă de utilizat dacă traiectoria punctului este cunoscută dinainte.

15. 1.2 Viteza punctului

Luați în considerare mișcarea unui punct pe o perioadă scurtă de timp Δt :

viteza medie a unui punct într-o perioadă de timp Dt . Viteza unui punct la un moment dat

Viteza punctului este o măsură cinematică a mișcării sale, egală cu derivata în timp a vectorului rază a acestui punct din sistemul de referință luat în considerare. Vectorul viteză este direcționat tangențial la traiectoria punctului în direcția mișcării.

Desenați o diagramă a sistemului și marcați centrul de greutate pe acesta. Dacă centrul de greutate găsit este în afara sistemului obiect, ați primit un răspuns incorect. Este posibil să fi măsurat distanțe de la diferite puncte de referință. Repetați măsurătorile.

• De exemplu, dacă copiii stau pe un leagăn, centrul de greutate va fi undeva între copii și nu la dreapta sau la stânga leagănului. De asemenea, centrul de greutate nu va coincide niciodată cu punctul în care stă copilul.
• Aceste argumente sunt valabile în spațiul bidimensional. Desenați un pătrat care va conține toate obiectele sistemului. Centrul de greutate ar trebui să fie în interiorul acestui pătrat.

Verificați-vă matematica dacă obțineți un rezultat mic. Dacă punctul de referință se află la un capăt al sistemului, un rezultat mic plasează centrul de greutate aproape de capătul sistemului. Acesta poate fi răspunsul corect, dar în marea majoritate a cazurilor acest rezultat indică o eroare. Când ați calculat momentele, ați înmulțit greutățile și distanțele corespunzătoare? Dacă în loc să înmulți ai adăuga greutățile și distanțele, ai obține un rezultat mult mai mic.

Corectați eroarea dacă ați găsit mai multe centre de greutate. Fiecare sistem are un singur centru de greutate. Dacă ați găsit mai multe centre de greutate, cel mai probabil nu ați adunat toate momentele. Centrul de greutate este egal cu raportul dintre momentul „total” și greutatea „totală”. Nu este nevoie să împărțiți „fiecare” moment la „fiecare” greutate: astfel veți găsi poziția fiecărui obiect.